曹睿

论文下载地址：http://proceedings.mlr.press/v97/guo19b.html

Slider下载地址：https://icml.cc/media/Slides/icml/2019/grandball(13-09-00)-13-09-35-4778-exploring_inter.pdf

代码下载地址：https://github.com/weilai0980/MV-LSTM

论文信息：论文发表于ICML2019，作者Tian Guo (ETH)，Tao Lin (EPFL)，Nino Antulov-Fantulin, (ETH)。

1. 论文摘要（包括论文动机、创新点或者贡献，论文的结论等）

对于按时间顺序训练的具有目标变量和外生变量的递归神经网络，除了要进行准确的预测以外，还需要对数据和模型提供可解释的见解。本文拓展了LSTM的结构，以学习variable-wise的隐藏状态，目的是捕获多变量时间序列中的不同动态，并区分变量对预测的贡献。利用这些variable-wise的隐藏状态，提出了一种混合注意机制来模拟目标的生成过程。然后，开发了相应的训练方法，以共同学习网络参数，变量及时间重要性，而无需预测目标变量。通过真实数据集上的大量实验捕获不同变量的动态性证明了本文提出的方案拥有更好的性能。同时，本文定性和定量地评估了解释结果。长远来看，它展示了作为对多变量数据进行预测和知识提取的端到端框架的前景。

论文的主要贡献：

• 拓展LSTM的结构掌握variable-wise的隐藏状态捕获每个变量的动态。它有助于预测和解释。这个LSTM家族被称为可解释的多变量LSTM，即IMV-LSTM。

• 设计了一种新的混合注意机制来总结变维后的隐藏状态，并对目标的生成过程进行建模。

• 提出了一种基于概率混合注意的网络参数、变量和时间重要性同时学习的训练方法。

• 针对统计、机器学习和基于深度学习的baseline，对IMV-LSTM进行了广泛的实验评估，结果表明IMV-LSTM具有优越的预测性能和可解释性。IMV-LSTM的思想很容易应用于其他RNN结构，如GRU和stacked recurrent layers。

2. 论文内容

当前的RNN由于其不透明的隐藏状态而无法满足对多变量数据的可解释性。具体来说，当对目标变量和外生变量进行多变量观察时，RNN及其变种模型会将所有变量的信息盲目地融合到用于预测的隐藏状态中，因此通过隐藏状态序列区分各个变量对预测的贡献是很难的。同时，个体变量呈现出在时间上不同的动态性，这些信息也被忽略了，从而妨碍了预测性能。

现有旨在提高RNN可解释性的工作中，很少涉及到RNN的内部结构，以克服多变量数据隐藏状态的不透明性。本文的目标是实现一个统一的预测和重要性解释框架，通过拓展LSTM结构和加入attention实现，命名为IMV-LSTM（Interpretable Multi-Variable LSTM）。下面从三个方面来介绍IMV-LSTM：

• IMV-LSTM的网络结构

IMV-LSTM的网络结构如图1所示，相比于传统的LSTM网络（如图2），IMV-LSTM为了获得variable-wise的隐藏状态信息，将原本D维的隐藏状态改为N*D维，这就意味着每个输入变量都对应了一行隐藏状态。

图 1IMV-LSTM with variable-wise hidden states

图 2Conventional LSTM with hidden vectors

具体来讲，IMV-LSTM的内部结果如图3所示。

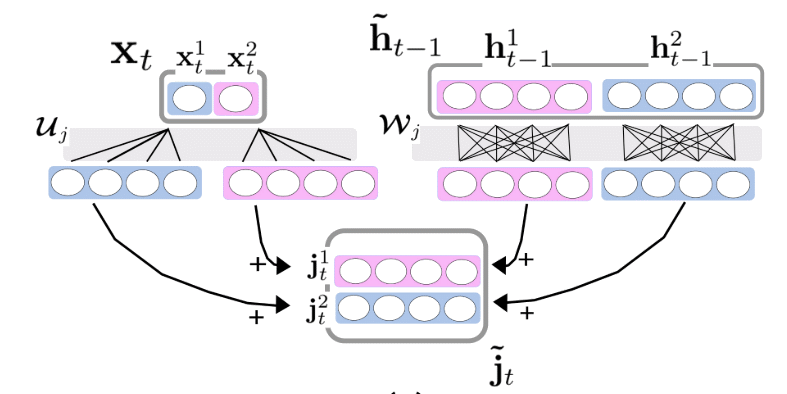
图 3IMV-LSTM network architecture

相比于传统的LSTM结构，INV-LSTM依然有输入门，遗忘门和输出门，只不过在更新存储信息时采用了新的方式，如公式（1）所示：

为了与传统的LSTM区分，IMV-LSTM中提出的新变量用~表示。根据门和存储单元的不同更新方案，文章提出了IMV-LSTM的两种实现，即方程组1中的IMV-Full和方程组2中的IMV-Tensor。在这两组方程中，表示向量化操作，它将矩阵的各列连接成一个向量。级联运算用表示，逐元素乘法用表示。表示将向量重塑为矩阵。

相比于传统的LSTM，IMV-LSTM在参数个数和时间复杂度方面都有减少。给定N个变量的时间序列，假设标准LSTM和IMV-LSTM层都具有D大小，即隐藏层有D个神经元。与标准LSTM的参数数量相比，IMV-Full和IMV- Tensor分别将每个时间步的参数个数降低了和，IMV-Full和IMV-Tensor在每个更新步分别具有以下计算复杂度：和。

• IMV-LSTM中的混合attention

混合注意力机制的思想如下。对每个变量对应的隐藏状态序列施加时间注意，以获取每个变量的历史记录。然后，通过使用历史记录的每个变量的隐藏状态，导出变量注意以合并变量状态，如图1右半部分所示。这两个步骤组合成一个概率混合模型，这有助于后续的学习，预测和解释。

混合attention可表述为：

这里，，由每个时间步attention对应输入变量的值和隐藏状态得到。在这个公式中引入了隐藏随机变量来控制生成过程，暗含的信息是T+1时刻当前的变量的输入变量的一种。

• IMV-LSTM如何预测和解释

在学习阶段，神经网络中的参数集和混合注意力由表示。给定一组个训练序列和，我们旨在学习参数和特征重要性向量和特征对应的时间重要性向量，以进行预测并深入了解数据。接下来说明直接解释注意力值，提出将参数和重要性向量学习相结合的训练方法，而无需进行后期分析。

针对公式（8），文章提出了新的损失函数如公式（9）所示：

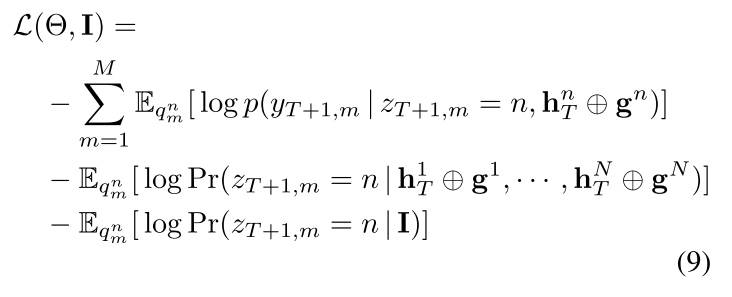
公式（9）的前两项是从标准EM程序派生。而最后一项是正则化项，它暗含的意思是鼓励各个实例遵循全局模式来估计特征重要性，下面给出和的计算：

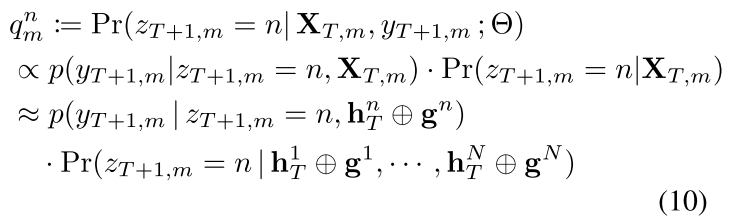
在训练阶段，可以交替学习网络参数和重要向量。在损失函数最小化的特定回合中，我们首先确定的当前值，然后为一批数据评估。然后，由于损耗函数中的前两项仅取决于网络参数，因此它们会通过梯度下降最小化以更新。此过程反复进行，直到收敛为止。训练后，获得了可供预测的神经网络以及变量和时间重要性向量。然后，在预测阶段，通过均值的加权和获得预测：

论文通过在三个数据集上的实验证明，IMV-Tensor相比前人的工作，模型性能最好。在变量和时间重要性解释方面，IMV-LSTM的结果也跟实际贴合，并给出了可视化的结果。具体的实验结果可参考论文，这里不再赘述。

3. 自己的认识和体会（包括与自己工作的联系和启发等）

模型可解释性是如今人工智能领域研究的热点。文章提出来的IMV-LSTM不仅可以提供特征和时序方面的可解释性，更重要的是这是一个端到端的架构，是在模型训练的过程中获取的可解释性，而不是后解释方案。我们实验室有许多跟时序相关的工作，因此该方案可以给各个研究小组提供新的研究思路。

但是论文的工作有一个重要的缺点就是每个输入变量之间是割裂的，模型没有考虑输入变量之间的影响。