王灿灿

论文下载地址：https://eprint.iacr.org/2016/799.pdf

论文发表在CCS 2016；

作者信息：Vladimir Kolesnikov,    Ranjit Kumaresan,   Mike Rosulek,  Ni Trieu  

Bell Labs,              MIT,             Oregon State University

1. 论文摘要（包括论文动机、创新点或者贡献，论文的结论等）

隐私集合求交（PSI）是密码学中一个非常有趣和重要的问题。而OT协议是PSI问题中的一个重要模块。本文描述了一种轻量级的协议，可以在存在半诚实的对手的情况下对伪随机函数（OPRF）进行不经意计算。在OPRF协议中，接收机的输入为r；发送方获得输出s，接收方获得输出F（s，r），其中F是伪随机函数，而s是随机种子。该协议在用于生成大量OPRF实例时特别有效。实现m个OPRF实例的成本大约等于之前实现3.5m个标准OT实例（使用最新的OT扩展）的成本。本问的OPRF可用于消除其PSI协议对各方项目的位长的依赖。基于本文OT协议的PSI协议的速度比Pinkas等人快3.1–3.6倍。无论元素的位长如何，本文协议仅需3.8秒即可安全地计算220个大小集的交集。对于非常大的集合，本文的协议仅比PSI的不安全的纯哈希方法慢4.3倍。

二、论文内容

本文提出了一个高效的隐私集合求交协议。

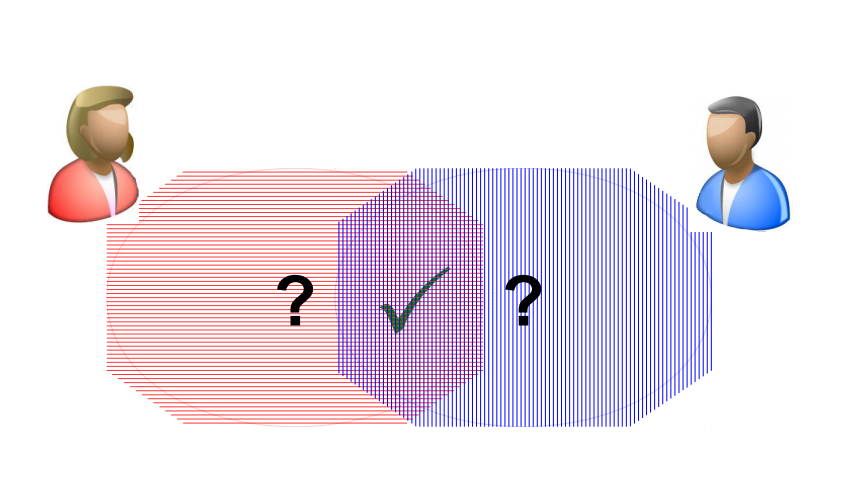
隐私集合求交是密码学中一个非常有趣的问题。以一个简单的场景为例，来看看什么是隐私集合求交。例如，幻灯片上有两个参与方：Alice和Bob。每个参与方都有一个集合，这里分别是 X 和 Y 。他们想计算两个集合的交集，但不想泄露其它额外的信息。例如，Alice不能知道Bob集合中非交集的元素。Bob也是类似的，他不能知道Alice集合中非交集的元素。这就是隐私集合求交问题的定义。

隐私集合求交的应用场景非常广泛，比如通讯录匹配场景。例如，Alice有一个手机，里面存储着Alice的通讯录，Alice想要使用Skype。另一边，Bob是一个Skype服务器，里面存储着客户数据。现在，Alice希望知道她的哪些朋友使用Skype，她希望使用Skype与朋友们聊天。很明显，两方希望计算集合的交集。然而，Alice不想泄露自己的通讯录，因为这是她的个人信息。Bob也面临类似的问题，他不能泄露自己的客户数据，因为这是客户的隐私。这个场景就需要使用隐私集合求交功能。

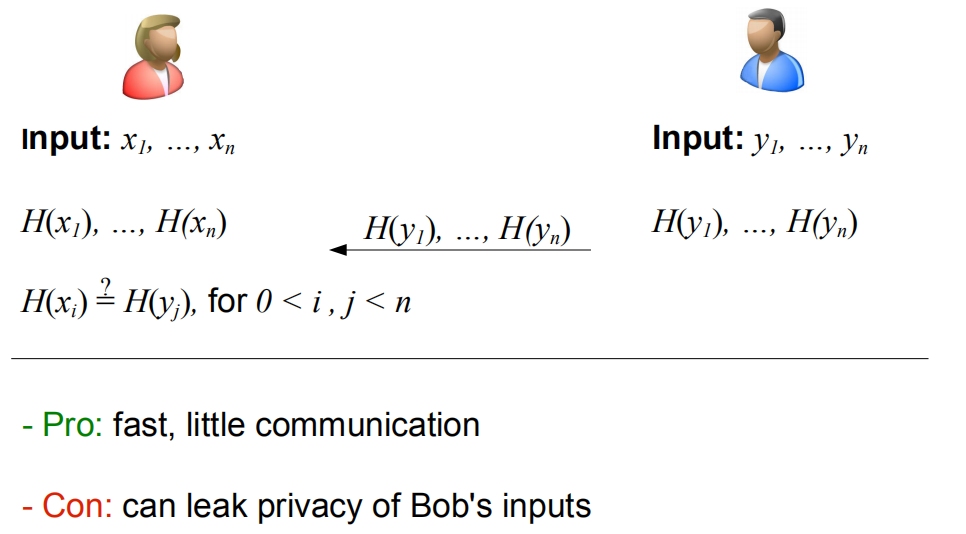
当考虑隐私集合求交这个问题时，我们可能会提出上述解决方案。Alice拥有集合  ，Bob拥有集合  。他们分别对  中的元素求哈希，对  中的元素求哈希。Bob随后将哈希值发送给Alice。Alice对比两个集合的哈希值，并输出哈希值相等的元素，即交集元素。这个协议效率非常高，因为协议只涉及到哈希值的计算。协议涉及的通信量也很小。但不幸的是，这个方案是不安全的，因为这个方案会泄露Bob输入集合的隐私。为什么呢？如果 Y属于比较小的域，例如 Y为电话号码，只包含大约10个数字，Alice直接计算上亿个电话号码的哈希值，并将结果与从Bob收到的结果对比。这样，Alice就可以知道Bob的输入了。这也是此协议被称为朴素哈希的根本原因。因此，这是一个不安全的PSI协议。

为了解决这个问题，学者们提出了很多PSI协议。当前最先进的PSI协议由Pinkas、Schneider、Segev和Zohner在2015年提出。隐私集合求交场景下的特殊情况为隐私相等性检测，即两个参与方希望知道两个字符串是否相等。他们的PSI协议通过不经意传输扩展实现隐私相等检测。他们还提出了一个高效的哈希技术，可以将隐私相等检测高效转换为隐私集合求交。本文的核心技术贡献是提高隐私相等检测的效率。

我们来看看Pinkas、Schneider、Segev、Zohner提出的隐私相等检测协议。Alice拥有 x，而Bob拥有y。我们想知道 x=y是否成立。他们使用了一个安全的黑盒工具，此工具叫不经意传输。Bob分别为0和1随机采样两个 L比特长的字符串。随后，Bob和Alice执行不经意传输协议，Alice的输入是她的第一个比特0。协议执行完毕后，Alice收到她第一个比特0所对应的字符串0。然而，Bob无法得知Alice在不经意传输中的输入是什么，此性质由不经意传输协议的定义所保证。他们继续对第二个比特、第三个比特执行此种操作。现在，Bob从OT协议中取得自己输入所对应的字符串。他的输入比特是011，因此他分别取得0、1、1所对应的三个字符串。他对几个字符串求异或，将结果发送给Alice。Alice也取得OT执行完毕后的结果，即0、0、1所对应的三个字符串。她对几个字符串求异或，并对比Bob发送过来的异或值。这样Alice就知道双方的输入是否相等了。这就是当前PSI协议的隐私相等检测过程。

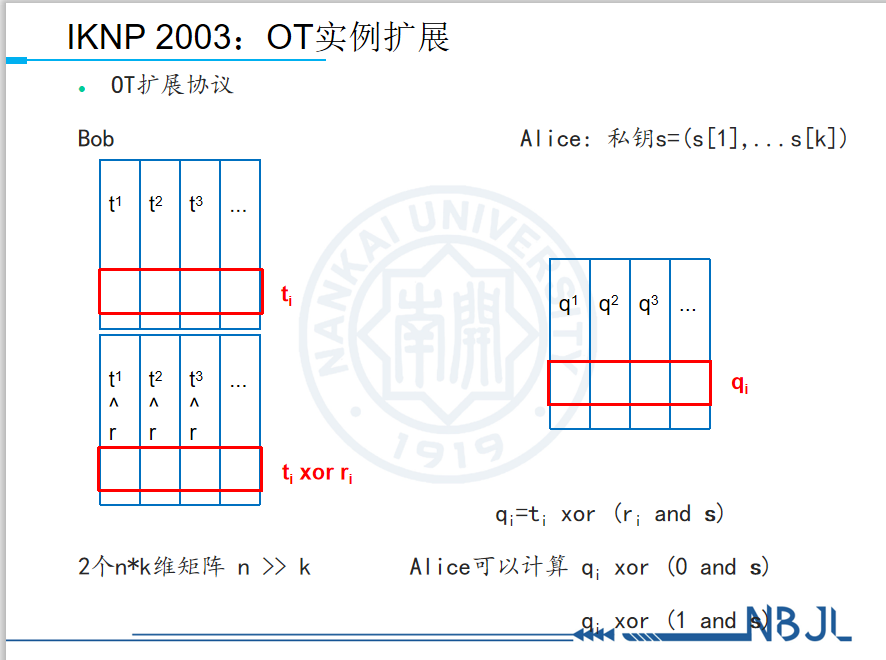
OT扩展协议的基本思想是，可以用少量OT和对称密码学操作构造大量的OT实例。Beaver在数十年前首次提出了这个想法。IKNP2003协议的基本思想是，在基础OT协议中，Alice选择一个随机的m比特长字符串t¹。她计算得到另一个字符串 t¹ xor r。在另一端还有个参与方Bob，他有一个单比特字符串 s₁。如果  s₁=0，则Bob接收到第一列字符串t¹。否则，Bob接收到第二列字符串 t¹ xor r。现在，他们重复上述过程k次，每次都使用相同的 r。最后，Bob收到包含 k列的矩阵Q，每列qⁱ的值都由比特 s_i所决定。现在，他们使用轻量级的密码学技术伪随机数生成器将 k个OT扩展为m个OT。这里 m要远远大于 k。

如果我们从行的角度观察这3个矩阵。记这三个矩阵的第i行分别为t_i、 t_i xor r、 q_i如上图所示。可以得到表达式 qi=ti xor (ri and s)。这里一个非常重要的性质是， ti=qi ，或者ti=qi xor s ，具体等于什么取决于ri。也就是说， qi 和 qi xor s有且仅有一个值等于ti，而另一个值对Alice来说看起来像随机数。换句话说，Bob有两个值，Alice只知道其中的一个值。

在2013年，Kolesnikov和Kumaresan指出，IKNP协议中包含重复编码。如果称 C 是一个 k个比特值重复编码 k次的编码过程，我们再来研究一下IKNP协议。第二个矩阵的第 i行等于ti xor C(ri) ，而qi=ti xor C(ri) and s。Bob计算的是qi xor C(0) and s和qi xor C(1) and s这两个值的哈希值。

现在，如果把随机编码移除，将 C替换为纠错编码，则此协议可以支持长度最大为8比特的选择比特值ri 。这也是为什么当前PSI协议只能对比8比特长的x和8比特长的y。举例来说，我们令 ri 的输入为3比特长，此时Bob需要根据幻灯片上的公式计算8个哈希值，而Alice只能得到其中一个哈希值，这也是为什么此协议被称为N选1-OT的原因。从安全角度看，他们的协议要求 C(ri) xor C(ri’)的汉明重量要大于k 。

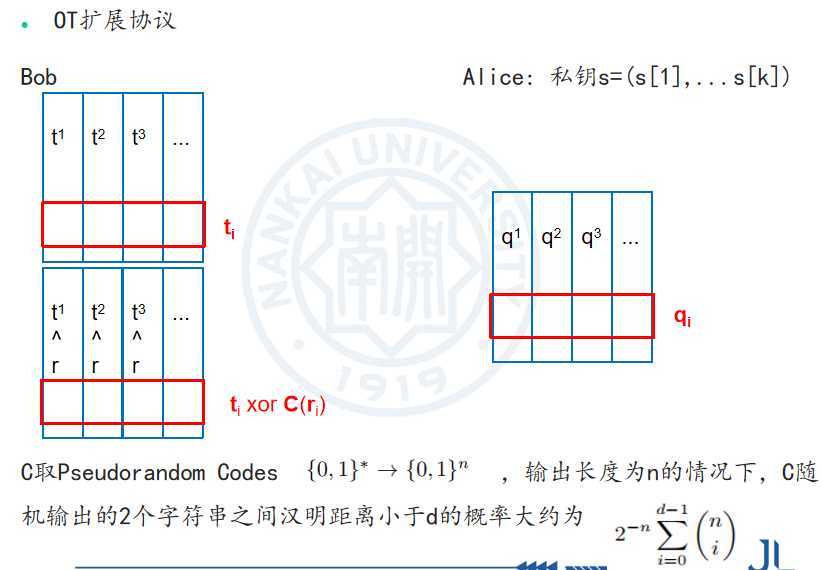
本文发现协议中不需要使用编码算法，可以将C 替换为输出k比特长随机字符串的随机函数。如果将C替换为随机函数，则协议可以支持任意长度的 ri。也就是说，这里的 ri可以为任意比特长。从Bob的角度看，他可以计算得到 qi xor C(ri’) and s 。Bob可以计算任意哈希值，而Alice只能知道其中一个哈希值。这就是为什么称该协议是∞选1-OT扩展的原因。从安全性看，要计算 C的最优输出比特长度，让此长度等于128，从而得到安全性。

在这里，C是一个Pseudorandom Codes ，输出长度为n的情况下，C随机输出的2个字符串之间汉明距离小于d的概率大约为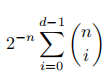，我们需要保证这个值是可忽略函数即可。由此式可以推出C的输出长度大约需要128*3.5 ---- 128*4 bit。

本文的PSI协议如上图所示。双方采用cuckoo哈希技术对各自的集合进行重排序，以减少元素比较次数，得到一个1.2n+s大小的哈希表。然后双方利用前面介绍的OT扩展协议得到1.2n+s个OT实例。Alice会利用这些OT实例结合自己的集合元素计算对应的哈希值，并将这些哈希值返回给Bob。最后Bob会利用自己已知的哈希值进行比对检测，以判断自己集合中对应的元素是否属于交集。

一些PSI协议的效率对比如上图所示。横坐标是运行时间（计算开销），纵坐标是通信量。

三、自己的认识和体会（包括与自己工作的联系和启发等）

CCS 2016上的这篇文章可以说是非常有代表性的PSI方案构造。方案综合使用了不经意传输、不经意传输扩展（Oblivious Transfer Extension，OTE）、Cuckoo哈希、不经意伪随机数生成器（Oblivious Pseudo-Random Generator），同时还引入了编码理论相关的知识，可以说是多种密码学技术和安全多方计算技术的集合体。