崔雯雯

论文下载地址：https://dl.acm.org/doi/abs/10.1145/3299869.3319860

论文信息：

    发表时间：2019

    会议名称：SIGMOD

    作者：Galakatos, Alex, et al. 

1  论文摘要（包括论文动机、创新点或者贡献，论文的结论等）

本篇论文主要讲述在数据库中，如何通过数据分布构建分段线性函数，利用key值查到元组存储位置的索引结构。在数据库中，以树为基础的索引结构帮助数据库管理员提升分析和事物装载性能，但是在大量的数据集上进行构建索引会消耗大量的内存，大概会占用55%的可用内存。这样不仅占用内存还限制了新数据的保存和立即处理现用的数据。对于这种问题，传统的解决方法，比如说针对于B+树的存储的压缩技术，主要通过减少在关键字之间的冗余或者减少每个节点内部关键字的大小。比如说，预剪枝和后剪枝。霍夫曼编码也可以应用到每个节点中。但是这些方法同时也会带来一些挑战，比如说，压缩结点后，在查询某个item的时候就会要先解压缩整个page后，才能查询，增加了运行时间。对于关键字增长速度很快的数据集，这种方法的效果就不怎么样了，比如说以时间戳为关键字，因为这种数据基本上是随着时间而增长的，导致索引的大小也会持续增长。而数据库管理员对于这种增加基本没什么办法，只能将完整的索引drop掉。

所以本文的作者，提出了一个新颖的索引结构：fting tree，fiting tree按数据趋势在一些基础的索引结构上（比如b+树）构建分段的线性函数使得能快速地找到元素位置的同时降低索引的内存消耗。，fiting tree在构建时受到一个可调参数error的限制，error主要是用来调节查询性能和空间消耗的平衡。同时作者还提供了一个评估模型对一定的查询延迟需求或者存储预算选择合适的error。

实验证明，这种新型的索引结构可以在保证查询和插入性能的同时，有效降低索引大小。

2 论文内容

OverView

接下来是讲解整体的构建思路，以及对那些是主键的属性（比如说学号）和不是主键的属性（比如说年龄）,分别让这个属性作为key值进行索引的构建。

首先索引可以由一个函数映射一个key到存储位置来表示，通过此种方法，FITing TREE将key值空间划分为几个不相邻的线性段去近似真实的这个函数。因为不可能通过一个模型就能完全拟合数据分布。其中关键的思想，是将索引构建为一个单调递增的函数，我们就可以使用函数将key映射到其存储空间了。为了解释这种想法，我们假设数据是根据key排好序存储在一个数组中，使用数组中的下标代表它的存储位置。我们以一个学校中教学楼的门把手的探测器的数据作为例子，其中蓝线为真实值，红线为预测值，横轴是key值，纵轴是这条数据的存储位置，我们以事件的时间戳作为key值并排好序，这个数据集中也遵循一定模式，比如凌晨的时候和周末的时候因为很少人去学校，所以数据量就变小了，增长的速度也变得缓慢了。

在每一段的线性函数中，预测的值为一个近似的值，而不是准确值。目标就是找到近似的线性函数能映射key到存储位置。线性的主要是出于计算和构建上的考虑。

     整个过程的核心主要是同一个可调参数error，error表示预测位置和真实位置的误差的最大值，也就是说，在这些分段线性函数中，最大误差应该不超过这个error。同时，fiting tree在构建时的核心块我们成为segment。在每个叶节点指向一个segment，在叶节点中，只存储每个线性segment的起始的key和线性函数的斜率，用来计算每个落到此叶节点中的key值的近似位置。

接下来，介绍如何构建不同的属性的索引结构。对于主键的属性（比如学号），首先也是将key值排序，每个segment对应着一个线性函数，叶节点存储每个segment的起始key和斜率和指向segment的指针。我们可以看到FITing Tree索引中，由于分割过程中数据的分布和error的设置，每个segment的大小是不同的，但是在传统的B+树索引中，叶节点指向的一个固定大小的page。

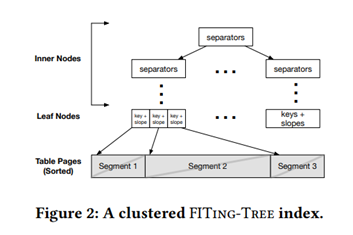
二级索引主要是为了提升涉及那些不是主键的属性的查询和插入性能，否则需要遍历所有的元组才能处理一些query。与一级索引不同之处是增加了一个间接层，这个间接层是将这些不是主键的值排好序后，在segment中存储指向这条元组的指针。也就是说segment中是排好序的。

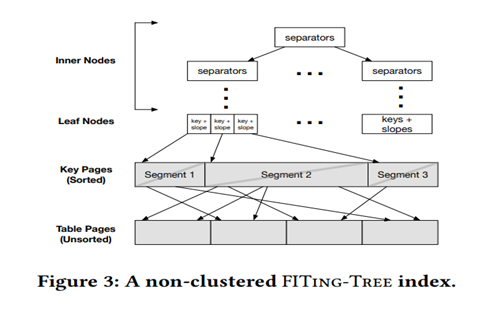
Segmentation

接下来讲解一下，这些segment是如何构建的。构建一个线性函数就需要一个目标，在这个地方，最小平方误差显然不太适用，因为最小平方误差并不能保证预测值和真实值间最大的那个误差是多少，因此也不能保证在构建segment时，最大误差不超过error。所以，segment构建时的的目标是能满足最大的误差不超过设置的参数error。

整个算法在构建时只需要遍历一遍数据集，所以时间复杂度为O(n),它的主要思想是一个key当且仅当不违反误差约束才能加入一个segment，否则重新建立一个segment。初始时，有一个Slope high设为无穷，Slope low取0（分别对应算法1、2行），取第一个key直接进segment，然后取第二个key，如果这个key在这个cone里面（也就是在slope high 和slope low夹住的这个范围内），则将这个key加入segment中，然后根据第二个key的位置加减error，得到有一个范围，更新slope high和slope low，如果新进来的key不在这个范围内，则重新以其为起始点建立新的segment。如右图，point 1是第一个key，直接加入，point 2进入后，在这个直角范围内，然后根据加减error的的范围更新slope high和slope low，虽然看point 3 和point4 以此类推。最终线性函数就在slope high和slope low之间选择，或者重叠。

    Segment如何构建说完，我们就可以说下，如何在这个索引结构中进行元素的查询和插入了。首先，由于本篇文章的Fitingtree是以b+树为基础构建的索引，所以首先要对b+树进行搜索查询到其所在的叶子节点，然后再通过叶子节点中segment的起始key值，斜率查到近似的位置，再其上下error个位置再进行查询。

相比于查询操作，插入操作就麻烦一点，在fiting tree中，作者不采用新插入一个数据就重建segment的原则，为了减少每个segment里面key值移动的次数，提高性能，而是在每个segment后加入一个固定的buffer，对于新插入的值，就有序插入进buffer中，当新插入的数据量达到buffer的大小时，则重新使用前面的算法构建segment，重新构建后的segment可能还是1（如果新加入的值不违反error）也有可能变为几个，新构建的segment再重新插入进tree中，旧的就会被移出。为了保证，查询时，能够正确查询到buffer中的元素时，在构建的时候，我们选择的error应该为（原本的error值-buffer的大小）。

Cost Model

因为error的值不仅影响查询和插入的性能同时还影响索引的大小。对于特定的事务装载workload，如何选择合适的值来适应不同需求。作者提供一个cost model来选择一个好的error以应对不同的需求。主要有两个指标需要优化：一个是查询延迟和空间的消耗。

不同应用有不同的查询延迟的需求，因为FITing Tree里面主要是error的选值来影响性能，所以为了满足特定的需求就应该选择合适的error。首先我们使用S_e来代表使用error e而构建得到segment的数目。总体的延迟估计得公式主要由先在树中找到对应的叶子节点的时间加上在segment中的查找时间再加上在buffer中查找的时间组成。并且在满足latency时，应该选择使得构建的索引大小最小的那个error阈值。

在数据库管理系统中，除了查询延迟的需求，对于索引的大小也有一定要求。目标：在不超过特定的索引大小时性能（比如查询延迟）达到最好。可以使用以下的函数来评估固定的error阈值下的索引大小。第一个部分是tree的大小，是树大小的上界，叶节点和内部节点，16b是key和指针的大小。第二部分是叶节点内部存储的起始key值，slope，和指向segment的指针。同样地，对于error的选值也是在满足size的需求使，选择使延迟最低的那个error。

Evaluation

接下来是使用实验对整个算法进行评估。首先进行查询的评估。在这个地方使用三个数据集，分别是微博，lot sensor和地图的数据。前两个数据集都已时间戳作为属性的key值，地图以维度作为属性key值，因为不是主键，所以是一个二级索引。

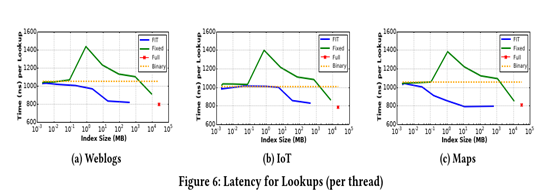
这里比对随着index size的增长，查询延迟的变化。其中蓝线是FITing tree，绿色的是使用固定大小的page的B+Tree索引，红色的是整个数据全部用来构建索引的B+树索引（全部加载进内存中），黄色的是不构建索引，而是通过使用二分查找在整个数据集上进行查找（对比二分查询主要是对比FITING tree的极端情况，就是只构建一个segment时，它的索引大小一直为0）。其中影响FITing Tree索引大小是error的选择，影响绿色的固定page的B+树索引的主要是固定page大小的选定。从图中可以看出，对于full index的查询时间是最小的，但是占用的内存空间也是最大的。二分查找随着索引大小的变化性能不怎么改变。首先只有Fit tree 和绿色的固定大小page的查询时间在随着索引大小变化。也可以看到，fiting tree在索引大小的更小的时候可以达到其最优的查询时间且很接近于full index，并且总是比固定page大小的索引查询时间短。

然后是整体插入性能的对比，通过将Fitting tree和固定大小page的索引和full index对比Inset性能时，通过吞吐量来比对。如图所示，两种索引都比full index的写效率要低。fiting tree可以和使用固定大小page的index的不相上下，甚至我们可以看到在某些error值下，Fiting tree是要比固定page的index性能要好的。但总体上，Fiting tree插入的性能要比其他两个要差，主要是因为是写入buffer中，而后需要跟segment合并在一起。

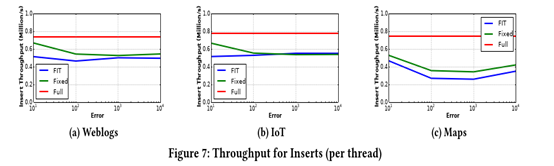
3  自己的认识和体会（包括与自己工作的联系和启发等）

     在面对实际的问题中，使用学习模型还是应该考虑尽量使用一些比较简单的模型，并且也应该根据实际需要去得到优化的目标。同时，在优化某些标准时（例如本文降低索引的所占内存），还需要保证这个结构本身的性能（例如，插入和查询）。